在前两次的巅峰对决(点击看量子纠缠上、下)中,以爱因斯坦为代表的经典物理学派一次又一次地向量子力学中的量子纠缠理论发出挑战,却被以波尔为代表的量子物理学派数次巧妙地化解危机。
这两大学派的巅峰对决不仅仅是物理学研究中的学术争论,也代表了经典时代和量子时代的不同思想的激烈碰撞。虽然波尔已经一次又一次巧妙化解了爱因斯坦的难题,但是经典物理学派的物理学家们还是在感情上难以接受微观世界中量子力学理论的思维方式。因此,当时两大学派之间的争论还未分出胜负。

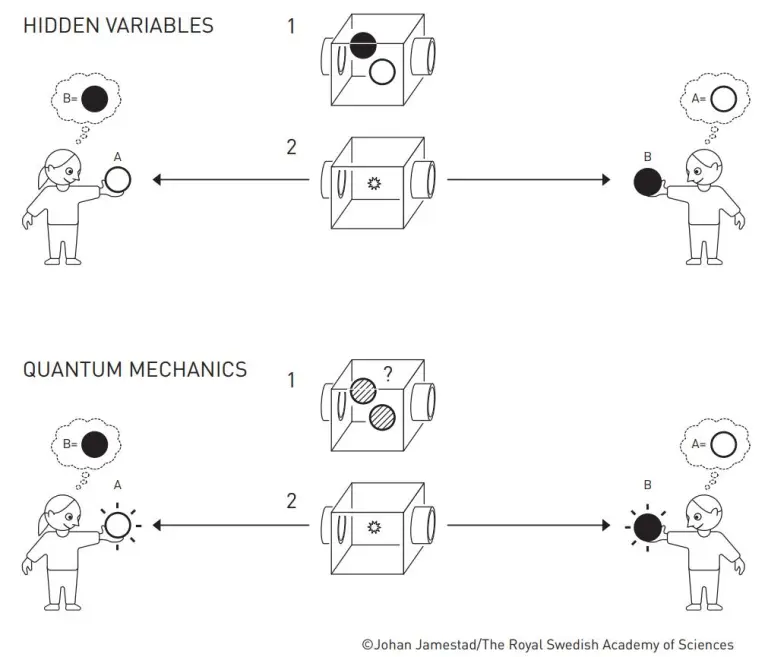
量子纠缠概念图(图片来源:veer图库) 在不断对决中,逐渐开始有物理学家想在经典物理学派和量子物理学派之间,寻找一个双方能够接受的折中方案。这样的话,既可以照顾到经典物理学派,又可以推导出量子力学中量子纠缠理论的合理解释。其中,最为知名的折中方案就是物理学家玻姆(Bohm)提出的“隐变量理论”。 隐变量理论——两大学派的折中方案 针对量子力学中对于微观世界的概率性描述,玻姆认为,量子力学中的量子纠缠理论应该是不够完备的。 很有可能,微观世界中概率性的背后隐藏着一个尚未被发现的变量,来影响人们对于微观世界的观测。也正是因为这个隐藏的变量还未被人发现,因此,我们只能感受到所谓的量子力学中的概率性。当我们发现其背后的“隐变量”之后,就可以避免任何概率性,或者不确定性。 心灵感应的示意图(图片来源:veer图库) 为了更加形象地理解隐变量理论,我们可以举一个宏观世界中双胞胎姐妹的例子,来类比解释一下背后的道理。 假如这对双胞胎姐妹长大后,无论她们两位相距多远,在某些特定的情况下,总是有可能做出一些相似的选择,也就是人们口中所谓的“心灵感应”,就像量子力学中的超距的相互作用一样,让人难以理解。 其实,这只是因为这对双胞胎姐妹拥有相近的基因,而她们生活中的各种表现往往受到基因的调控,进而影响到她们最终的选择。也就是说,人们眼中神秘的超距相互作用,其实很可能只是受到隐藏在她们体内基因的控制罢了。 处于“量子纠缠”的一对粒子 (图片来源:veer图库) 因此,只要找到量子力学理论背后的“基因”,也就是玻姆所提出的隐变量,就可以解释清楚量子力学中的概率性了。 虽然隐变量理论看起来十分合理,并且也暂时让经典物理学派和量子物理学派达成了和解。但是各位,我们是不是还遗漏了一个最重要的事情没有做呢? 那就是,物理的理论再完美,思想实验再有趣,总是需要用真实的实验来验证,才能一锤定音。而接下来敲下最后一锤的人,就是我们最后登场的物理学家贝尔(Bell)。 贝尔不等式——公正的裁决 如果只从感情的角度出发,物理学家贝尔还是更加倾向于以爱因斯坦为代表的经典物理学派。于是,他又开始重新审视之前的EPR佯谬,并且希望将这个思想实验进一步推进到一个可以被验证的物理实验,从而帮助解决两大学派几十年的争论。 贝尔与贝尔不等式(图片来源:Quantum Magazine) 如果按照爱因斯坦在EPR佯谬中的经典物理思维继续推导下去,可以这样来理解: 由于大粒子分裂成为A和B两个粒子,那么按照经典物理思维中的“确定性”思想来理解,A和B粒子的状态应该在分离前的那一刻,就已经被确定下来。 也就是说,如果经典物理学派的理论是正确的话,那么A和B粒子无论相距多远,应该始终相互关联,并且遵循经典物理的统计规律。这样一来,贝尔就可以通过这种经典的概率统计学计算,得到一个相应的不等式!


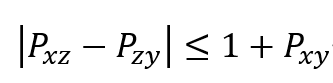
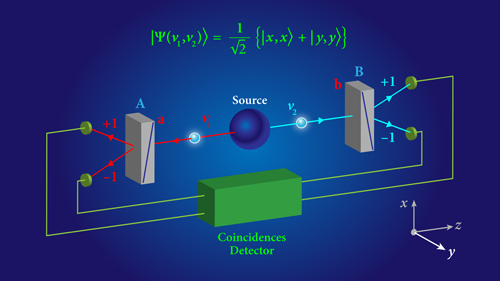
不等式中的x,y,z代表三维空间的三个观察方向,而概率P代表不同观察方向之间的关联。比如,Pxz代表从x方向观察与从z方向观察的关联性,如果观察的结果存在关联性,那么Pxz = +1,反之则为-1。因此,我们就可以在实验上来观察,A和B粒子在三个方向的关联性,从而验证上述贝尔不等式的是否成立。
“隐变量理论”与量子力学的示意图(图片来源:Johan Jamestad/The Royal Swedish Academy of Sciences) 由于贝尔不等式是从经典物理学派的理论出发得到的,因此,如果贝尔不等式在实验上被验证成立(即,不等式左侧<右侧),那么就说明经典物理学派的理论是正确的。反之,如果贝尔不等式在实验上被验证不成立(即,不等式左侧>右侧),则就说明量子物理学派的理论是正确的。 一锤定音——量子物理学派取得胜利! 其实,验证贝尔不等式所需要的实验条件过于理想化,比如严格意义上的关联性。因此,最初的贝尔不等式不适合真实的实验验证。 于是在1969年,物理学家克劳泽(Clauser)和合作者进一步发展了贝尔不等式,使得其更加适用于实际的实验验证,而这个不等式也被称为“CHSH不等式”。 而在1981—1982年,物理学家阿斯佩(Aspect)与合作者陆续完成了3次纠缠光子的实验,并且在实验上观察到了CHSH不等式的不成立(即贝尔不等式也不成立),但是仍然存在一些实验上的漏洞。 随后在1997年,物理学家塞林格(Zeilinger)带领研究小组进一步完善了纠缠光子实验,并且补上了全部的实验漏洞,以极高的精度验证了CHSH不等式的不成立(即贝尔不等式也不成立)。 在2022年,诺贝尔物理学奖授予阿兰·阿斯佩、约翰·克劳泽和安东·塞林格,表彰的理由是“他们利用纠缠光子进行实验,验证了贝尔不等式不成立,开创了量子信息科学”(点这里复习22年诺贝尔物理学奖)。 2022年诺贝尔物理学奖获得者(图片来源:The Nobel Prize) 具体而言,他们三位是根据EPR佯谬的思想实验,选用一对纠缠的光子作为A和B两个粒子,并且在相距很远的地方分别探测两个粒子的状态。在这里,我们不必要纠结光子是什么,只需要知道根据量子力学的量子纠缠理论它们两者之间可以处于量子纠缠的状态即可。 利用纠缠光子验证贝尔不等式的实验(图片来源:American Physical Society) 由于A和B粒子已经飞出很长一段距离,这时候实验上就可以同时触发两端的探测器,来同时测量两个粒子各自的状态。由于A和B粒子相距较远,即使是以经典理论中最快的光速,都无法短时间内传递两者之间的相互作用。 而当他们一次又一次重复实验后,最终发现,A和B两个粒子的确存在奇妙的关联,并且经过概率统计计算后的结果,也的确验证了CHSH不等式的不成立(即贝尔不等式也不成立)! 也就是说,经典物理学派的确错了,而且从经典物理学派的观点出发,来折中两大学派的隐变量理论也错了。因此,量子物理学派提出的量子力学的量子纠缠理论,虽然让人匪夷所思,但的确是正确的,微观的量子世界的本质就是概率性的!(点这里看诺奖得主深入解读量子世界 ) 结语 可以说,经典物理学派和量子物理学派的争论,是20世纪科学史上最伟大的事件。在一次又一次的巅峰对决中,量子力学的理论不断完善,现在已经成为高等学校物理学专业中的一门基本课程。 时至今日,仍然有很多的物理学家感叹这种“鬼魅的超距相互作用”,并且被量子力学的魅力所折服。其中,量子纠缠更是作为量子力学理论的核心,被大众所津津乐道。 量子纠缠示意图(图片来源:Johan Jamestad/The Royal Swedish Academy of Sciences) 此外,随着量子信息技术的不断发展,物理学家们也开始尝试利用量子纠缠的奇妙特性,进行远距离的保密通信。而这种利用量子纠缠进行传递信息的方式,也被形象地称为“量子隐形传态”。 可以说,量子力学深刻地改变了我们当今所处的世界,并且已经逐渐深入到我们的生产生活之中。“量子纠缠”的魅力,也仍然在吸引更多的人,来探索量子世界的奥秘。 作者:栾春阳 作者单位:清华大学物理系